
Name: Brandon Wong

Project 2 has multiple parts each with separate goals. Throughout the project, filters and frequencies are used to do accomplish a variety of different tasks.
In this part, I convolved the finite difference operators D_x = [1, -1] and D_y = [[1], [-1]] with the cameraman image shown above. This resulted in these two images:

Convolved with D_x

Convolved with D_y
I then combined the two images by computing the square root of the sum of the squares of the two images, resulting in the gradient magnitude image. Then, I binarized the image at the threshold of 0.3 to find the edge image with minimal noise.

Gradient Magnitude

Edge Image
In this part, I convolved the cameraman image with a gaussian created using the outer product of cv2.getGaussianKernel(15,2) to obtain a blurred version of the cameraman image. I then convolved this blurred image with D_x and D_y. These were then used to find the gradient magnitude image of the blurred image the same way as the previous part, and then this new gradient magnitude image was used to find the new edge image using the threshold 0.05, much smaller than in the previous part. Another difference was that the lines of the edge image became thicker in the edge image of the gaussian-blurred cameraman image compared to the unblurred version.

Blurred Convolved with D_x

Blurred Convolved with D_x

Blurred Gradient Magnitude

Blurred Edge Image
I also obtained very close results in a different way in this part. Instead of convolving the cameraman image with the gaussian, and then the D_x and D_y filters, I convolved the gaussian with the D_x and D_y filters to obtain the Derivative of Gaussian (DoG) filterns, and then convolved the cameraman with those resulting filters. This way, the cameraman only needed to be convolved with once for each filter result. The rest of the steps were the same, with a threshold at 0.05 again.

Convolved with DoG_x

Convolved with DoG_x

DoG Gradient Magnitude

DoG Edge Image
In this part, I sharpened two images the given taj image and an image of a bowl of salmon and rice I had for dinner the other day. The images were sharped first by convolving them with a gaussians made from the outer product of cv2.getGaussianKernel(15,2) to obtain their low frequency versions. These low frequency versions were then subtracted from the original image to obtain just the high frequencies. The high frequencies were added to the original images to make them clearer and sharpen the original image. All of these steps were combined into a single step in the form of the unsharp mask filter, where the original images were convolved with 1 plus an alpha value multuplies by the identity filter minus the alpha value times the gaussian filter. I always set alpha to 1, it was always enough.

Original

Low Frequency

High Frequency

Sharpened

Original

Low Frequency

High Frequency

Sharpened
The unsharp mask filter was also tested on an image that was blurred with the gaussian first. This image was of a crepe cake I made the other day. Unfortunately the original quality of the image could not be reobtained, and the new sharped image was decidedly worse than the original, with an odd shininess to it.

Original

Blurred

Sharpened
In this part I blended the high frequencies of one image with the low frequencies of the other to create a hybrid image, where the low frequency image is what is seen from farther away while the low frequency image is what is seen while close up. I did this with three images the given Derek and Nutmeg images, an image of a bowl of chicken mapo tofu I made the other day and an image of a bowl of broccoli chicken I made another day, and an image of a salmon avocado and kimchi sandwich I made the other day and an image of a steak sandwich I made another day. The hybrid of the bowl of mapo tofu and broccoli chicken was a failure. While you can see a larger bowl (the mapo tofu) from farther away, the contents of the bowls really only look like broccoli chicken with a single distinct piece of tofu no matter the distance. This was likeley because both images have chicken pieces around the same size, which makes it hard to distinguish them. The tofu isn't particularly distinctive from pieces of chicken either, and the broccoli's darker color and what makes is distinct close up and farther away. The

Derek

Nutmeg

Hybrid

Salmon Sandwich

Steak Sandwich

Hybrid

Salmon Sandwich Fourier

Steak Sandwich Fourier

Salmon Sandwich High Fourier

Steak Sandwich Low Fourier

Steak and Salmon Sandwiches Fourier

Mapo Tofu

Broccoli Chicken

Hybrid
In this part, I obtained the gaussian and laplacian stacks of the given apple and orange images. The gaussian stacks were obtained by repeatedly convolving the previous level with the gaussian formed from the outer product of cv2.getGaussianKernel(20, 20) to get the next level. The laplacian stack were generated by subtracting the previous level with the next level to find the difference between the levels. These stacks are displayed below.

Level 5

Level 4

Level 3

Level 2

Level 1

Level 5

Level 4

Level 3

Level 2

Level 1

Level 5

Level 4

Level 3

Level 2

Level 1

Level 5

Level 4

Level 3

Level 2
Level 1
In this part, I brought the stacks obtained through the methods in the previous part together to obtain the blended result of the two images based on input masks. The final blended images were obtained by summing up the laplacian stacks and their corresponding mask (obtained by convolving the mask of the previous level with a gaussian) up and then adding the final blurriest gaussian level multiplied the mask of its level on top of that. The two summed of separate stacks of the two different images were then summed together to obtain the final blended image, with the seam smoothed out. I did this on the given apple and orange images, an image from a breakfast taco I made the other day and a pot filled with mist from dry ice, and a different image of the same crepe cake from before and an image of cookie dough with a spoon in it. The last blended image is my favorite, it looks like the cookie dough is being spread over the crepe cake as frosting. The second two images have irregular masks, one with an oval and one with an oval with a rectangle sticking out of it. The results are shown below.

Apple

Orange

Orapple

Taco in Pot

Cookie Dough Frosted Crepe Cake
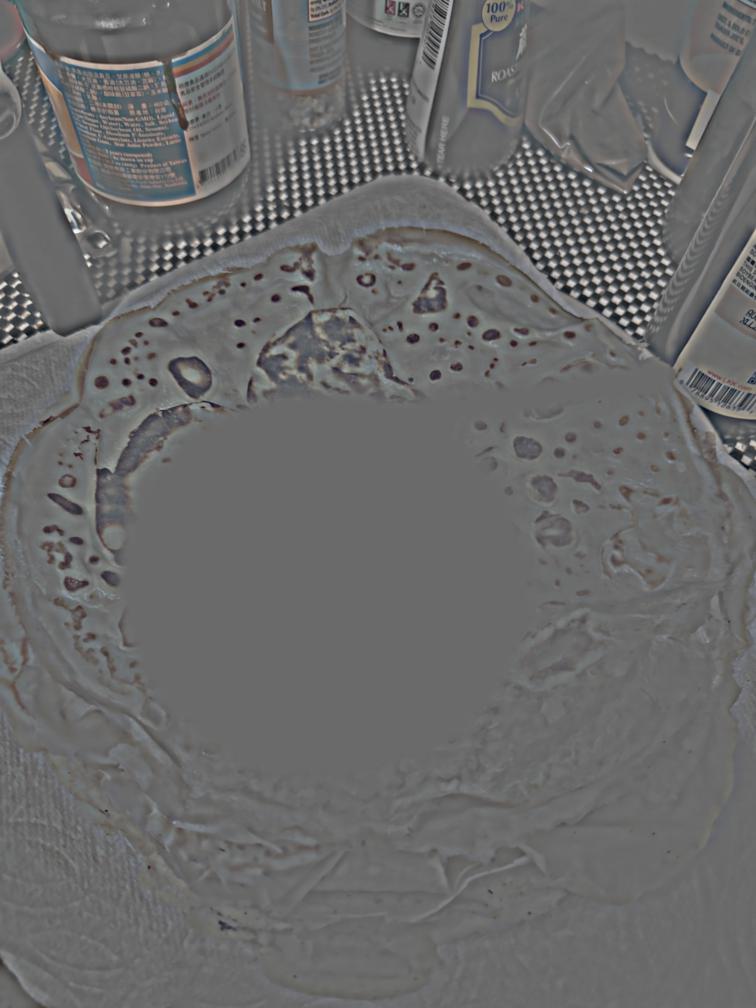
Level 5
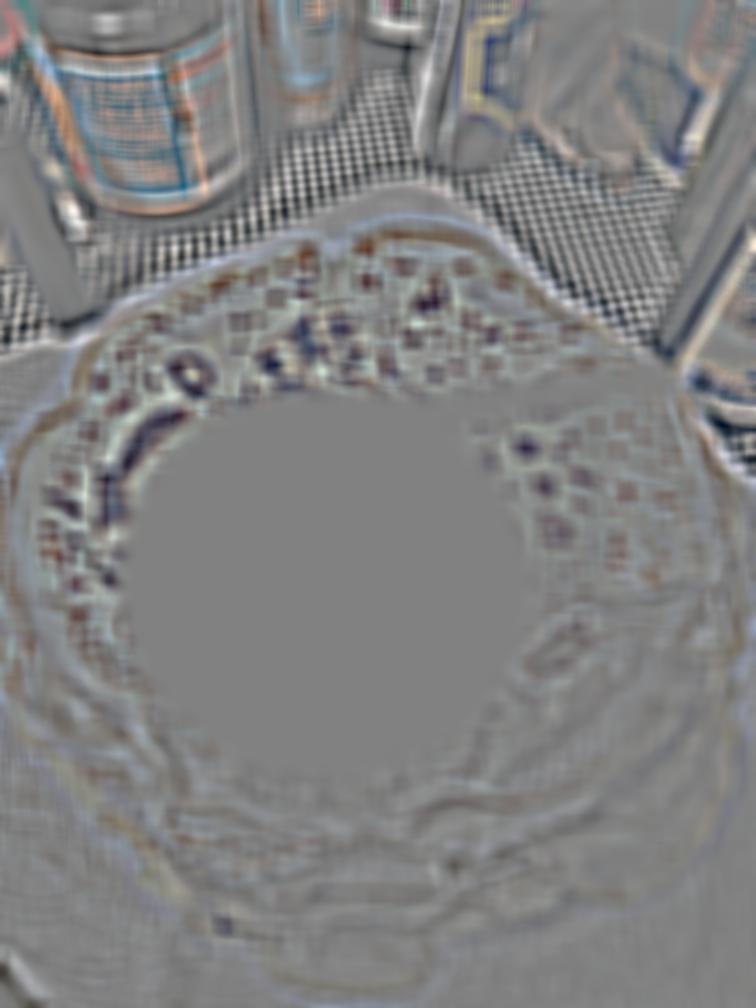
Level 4
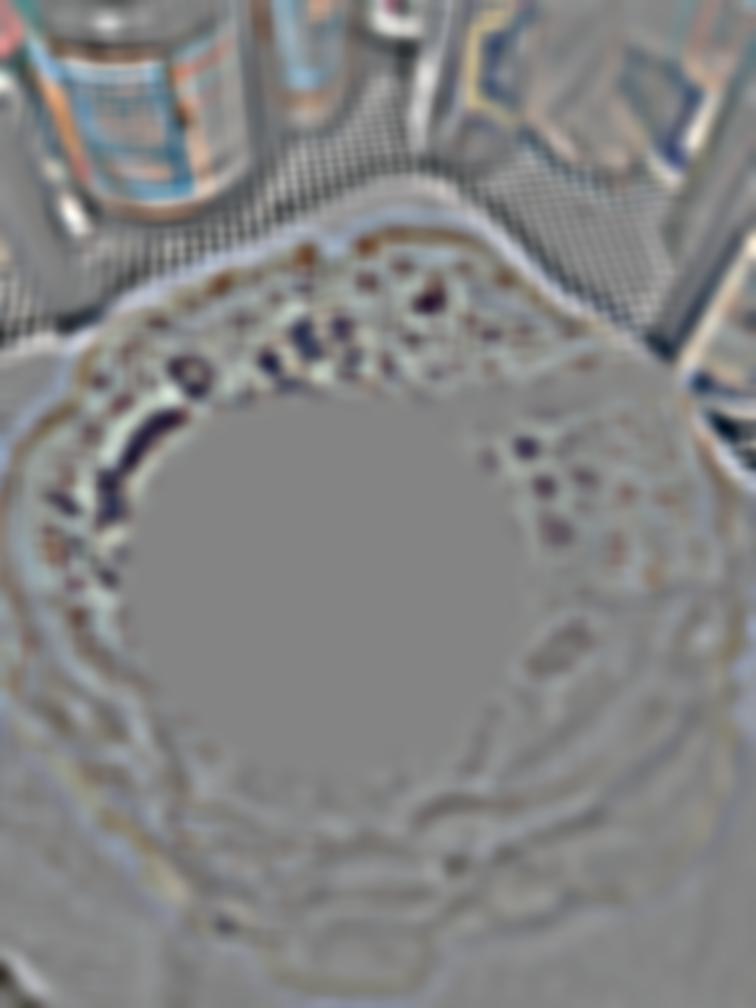
Level 3
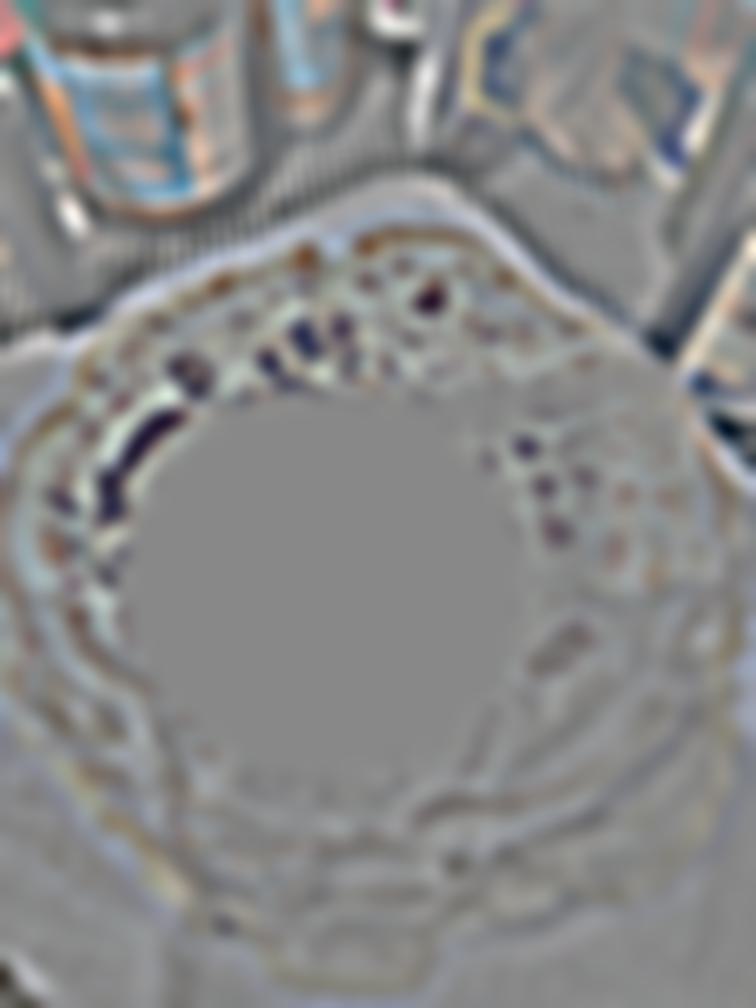
Level 2

Level 1

Level 0
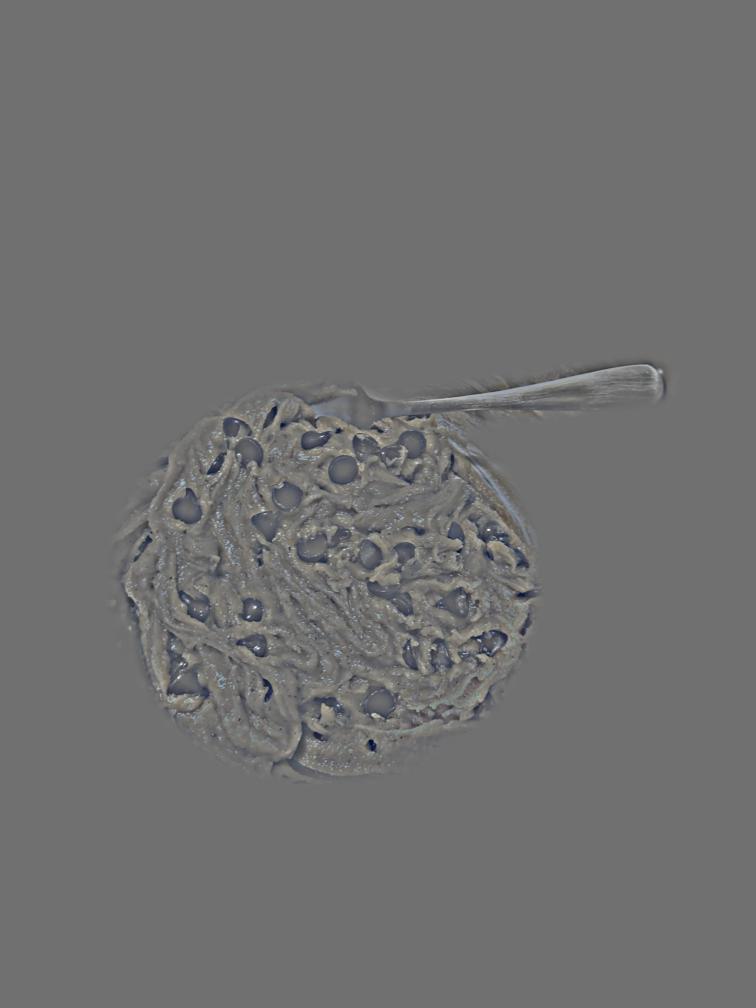
Level 5
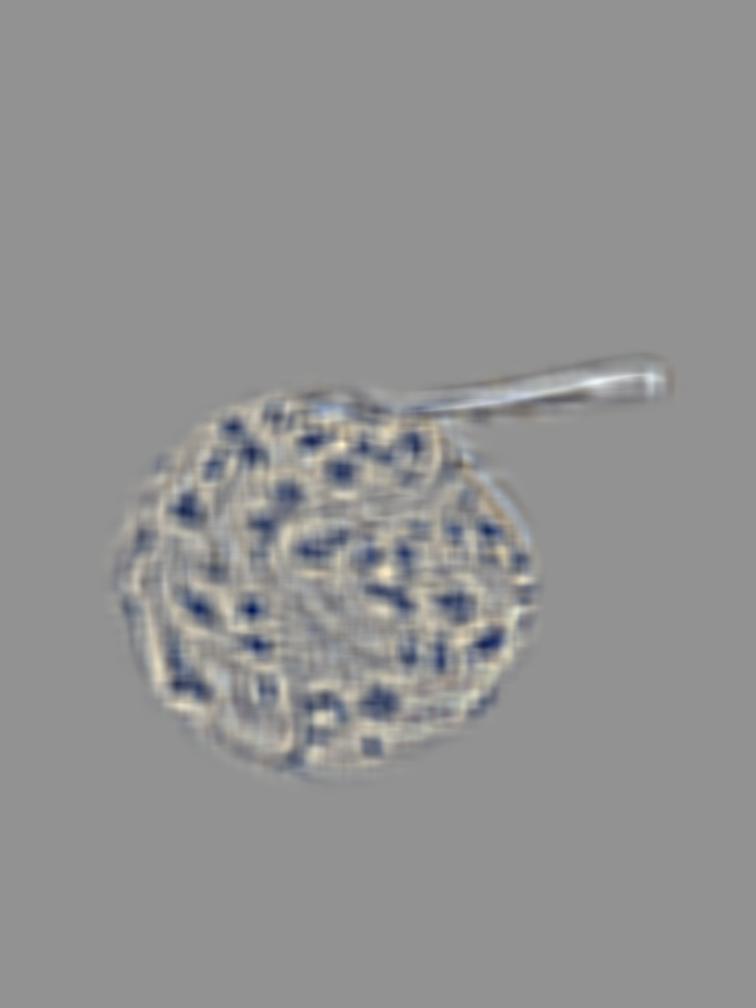
Level 4
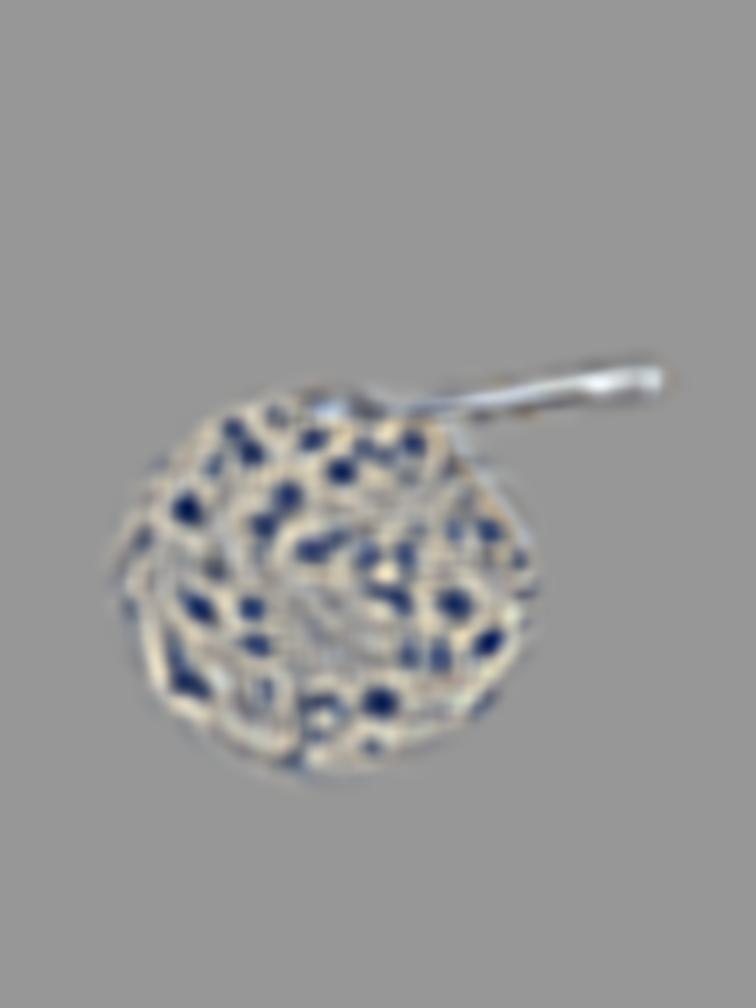
Level 3

Level 2

Level 1

Level 0
Level 5
Level 4
Level 3
Level 2
Level 1

Level 0